The Notebook interface is OK for quick calculations, but for more serious projects you will need to create files containing definitions of the functions that perform your calculations. To read in and execute a file containing mathematica commands:
<< mydefinitions.mMathematica searches for this file in the directories (folders) listed in the variable $Path.
In programs, you define functions using Module, and avoid using global variables as much as possible. For example, here is a function that calculates the moment of inertia of a sphere:
M$of$I$sphere[radius_,density_]=Module[{r$ax,z}, (* declare r$ax and z as local symbols, internal to the function *)
r$ax[z_]=Sqrt[radius^2-z^2]; (* you can define a function within a function *)
Integrate[ Pi/2 * density * r$ax[z]^4, {z,-radius,radius}]
];
M$of$I$sphere[R,rho] (* use the function *)
(8*Pi*rho*R^5)/15
All the symbols that we use temporarily inside the
module (r$ax and z in this case)
are declared at the start of the module as local variables.
This prevents interference with any global variable called z
or r$ax. We do not declare radius or
density as local because they are arguments to the
function we are defining.Within a function, you can use standard programming constructs such as for-loops, if-tests, and while-loops. When testing expressions you can use Boolean operators like
| "and" | && |
| "or" | || |
| "not" | ! |
First example: testing whether a list contains a given element. We define the function using delayed evaluation (
:=) because it cannot be evaluated until it is called with an actual list and element as arguments.
contains[list_,element_]:=Module[{i,found}, (* all variables internal to the function are declared as local *)
i=1; found=False;
While[i<=Length[list] && ! found, (* 'found' is a Boolean variable *)
found= (list[[i]]==element); (* As in C and Python, we use ==
for the equals sign in an equation *)
];
found (* returns a Boolean *)
];
contains[{4,9,2,8,1,-3}, -3] (* Use the function we have just defined *)
True
Second example: counting how many times a given element appears in a list:
occurrences[list_,element_]:=Module[{i,nfound},
nfound=0;
For[i=1, i<=Length[list], i++, (* As in C and Python, i++ and i+=1 both mean i=i+1 *)
If[ list[[i]]==element, nfound+=1];
];
If[nfound>0,
Print["found ",nfound," occurrences"]
,(*else*)
Print["found no occurrences"]
];
nfound (* returns number of occurrences *)
];
The Solve command attempts to find all solutions of an equation. For example, to find the two roots of a simple quadratic x^2 -c,
eqn = ( x^2 - c == 0 ); (* As in C and Python, we useWe see here that the Solve command returns a list of solutions. Each solution is itself a list of substitution rules, taking the form x -> EXPRESSION. To set some variable x$soln equal to the solution you have to apply the relevant set of substitution rules to the variable that was in the equation (x in this case).==for the equals sign in an equation *) rules$list = Solve[ eqn, x] {{x -> -Sqrt[c]}, {x -> Sqrt[c]}} (* There are two solutions in the list *) x$soln = x /. rules$list[[2]] (* to get the second solution, apply the second set of rules to x *) Sqrt[c])
For multiple simultaneous equations with multiple unknowns, give Solve a list of equations and a list of unknowns, and as before you'll get back a list of solutions, but now each solution will be a list of several rules, one for each unknown. Here is an example, written as a function,
twovar$root[c_] = Module[{x,y,eqn$list,rules$list}, (* all variables internal to the function are declared as local *)
eqn$list = { x^2 +y^2 == 2*c, x + y == 0};
rules$list = Solve[ eqn$list, {x,y} ]; (* solve the two equations for x and y *)
(* At this point, rules$list is {{x -> -Sqrt[c], y -> Sqrt[c]}, {x -> Sqrt[c], y -> -Sqrt[c]}} *)
{x,y} /. rules$list[[2]]
];
twovar$root[w] (* use the function we just defined *)
{Sqrt[w], -Sqrt[w]}
To slice out part of a list, use the ;; construction:
list1 = {1,2,3,4,5,6,7,8,9};
list1[[4;;8]]
{4, 5, 6, 7, 8}
The index -1 means the last element of the list, -2 means the next-to-last,
and so on:
list1[[5;;-1]] {5, 6, 7, 8, 9} list1[[-4;;-1]] {6, 7, 8, 9}Lists can be built using the Table function:
list2 = Table[ i, {i,1,9} ]
{1, 2, 3, 4, 5, 6, 7, 8, 9}
To populate lists with more complicated contents, we can use the fact that
anywhere a value is required, one can put a series of statements,
separated by semicolons, that yield
that value. For example, to make a series of {x,f[x]} pairs:
xy$list = Table[x=i/5.0; y=Tanh[x]; {x,y} , {i,0,10} ]
{{0., 0.}, {0.2, 0.197375}, {0.4, 0.379949}, {0.6, 0.53705},
{0.8, 0.664037}, {1., 0.761594}, {1.2, 0.833655}, {1.4, 0.885352},
{1.6, 0.921669}, {1.8, 0.946806}, {2., 0.964028}
}
In plots of functions, one can make one or both axes logarithmic:
LogPlot[ 1.5^x , {x,0,10} ] (* logarithmic y axis *)
LogLinearPlot[ Tanh[x] , {x,0.01,10} ] (* logarithmic x axis *)
LogLogPlot[ x^1.67, {x,0.01,10} ] (* logarithmic x and y axis *)
One can plot lists of (x,y) co-ordinates instead of functions:
xylist = Table[ x=i/10.0; y=x^2; {x,y}, {i,1,10} ] (* 10 points on the y=x^2 curve *)
{{0.1, 0.01}, {0.2, 0.04}, {0.3, 0.09}, {0.4, 0.16}, {0.5, 0.25}, {0.6, 0.36}, {0.7, 0.49}, {0.8, 0.64}, {0.9, 0.81}, {1., 1.}}
ListPlot[xylist];
Lists can also be plotted on logarithmic axes:
ListLogPlot[xylist]; (* y axis is a log axis *) ListLogLogPlot[xylist]; (* both axes are log *)To plot functions and lists on the same plot, use the Show function to combine the plots. In this case, when we create plot1 and plot2 we stop them from being displayed by setting the DisplayFunction to do nothing (
Identity), and then set it back to the default ($DisplayFunction) when we combine the plots using Show:
plot1 = Plot[ Cos[x*Pi/2], {x,-1,1}, DisplayFunction->Identity ];
xylist = Table[ x=i/10; y=1-x^2; {x,y}, {i,1,10} ];
plot2 = ListPlot[xylist,DisplayFunction->Identity ];
plot$12 = Show[plot1,plot2]; (* combine plot1 and plot2 on a single plot *)
Show[plot$12, DisplayFunction->$DisplayFunction]; (* show the combined plot on the screen *)
Export["plots_comb.pdf",plot$12] (* create PDF file of the combined plots *)
To control color, thickness, etc, use the PlotStyle option:
(* one plot style for one curve *)
Plot[ Cos[x*Pi/2], {x,-1,1},
PlotStyle->{Cyan,Thickness[0.007],Dashing[{0.03,0.03}]}
];
 |
(* list of plot styles for different curves *)
Plot[ {Cos[x*Pi/2],1-x^2*Pi^2/8}, {x,-1,1}, PlotStyle->{
{Cyan,Thickness[0.01],Dashing[{0.03,0.05}]},
{Purple, Thickness[0.005]}
} ];
|
For example, suppose we want a root of x^3 -Tanh[x]. We use FindRoot and tell it to search in the range x=0 to x=1.0:
x$rule = FindRoot[ x^3 -Tanh[x], {x,0,1.0} ]
{x -> 0.}
x$soln = x /. x$rule
0.
As with Solve, the result is returned in the form of a rule,
but FindRoot returns at most one solution, which in this case
may not be what was intended: there are two roots
in the range x=0 to 1, and FindRoot found the
trivial one. Specifying a narrower initial search range helps it find the
non-trivial solution:
x$rule = FindRoot[ x^3 -Tanh[x], {x,1.0,1.2} ];
x$soln = x /. x$rule
0.893395
Note that Mathematica will go outside the initial search range
(in this case x=1.0 to 1.2) if necessary.It is also OK to provide only one initial guessed value instead of a range.
For multiple simultaneous equations, just provide lists of expressions and variables. Here is an example, written as a function that is defined by delayed evaluation (:=) because FindRoot needs numbers to work with.
xy$solutions[x$guess_?NumericQ, y$guess_?NumericQ] := Module[{x,y,xy$rule},
(* we will explain below why the ?NumericQ
patterns are needed *)
xy$rule = FindRoot[ {x^3-Tanh[y], y - x^2}, { {x,x$guess}, {y,y$guess} } ];
{x,y} /. xy$rule
];
xy$solutions[0.7,0.5]
{0.853834, 0.729033}
Let's solve the time evolution equation for a classical harmonic oscillator, using the mathematica DSolve function.
eqn = ( D[theta[t],{t,2}] == -theta[t] ); (* or we could have written it as theta''[t] == -theta[t] *)
bc = {theta[0]==1, theta'[0]==0}; (* boundary conditions *)
soln$rules$list = DSolve[ {eqn, bc} , theta[t], t]
{{theta[t] -> Cos[t]}}
theta$soln[t_] = theta[t] /. soln$rules$list[[1]] (* there is only one solution, but we still have to specify the first solution *)
Cos[t]
DSolve returns a list (of length 1) containing a
list of substitution rules (see Rules... above), one
for each unknown function in the differential equation.
In this case there is one unknown function theta,
so soln$rules$list[[1]] is a list containing one rule
that replaces instances of the unknown theta[t] with the
solution to the differential equation.We then applied that rule to define theta$soln to be the analytic function which solves the differential equation.
theta$soln''[t] + theta$soln[t]
0
Let us again solve the time evolution equation for a classical harmonic oscillator, this time numerically using NDSolve,
SHO$solution[tmax_?NumericQ]:= Module[{eqn,bc,theta,t,soln$rules$list},
(* we will explain below why the ?NumericQ
pattern is needed *)
eqn = ( D[theta[t],{t,2}] == -2*theta[t] ); (* or theta''[t] == -2*theta[t] *)
bc = {theta[0]==0.5, theta'[0]==0}; (* boundary conditions *)
soln$rules$list = NDSolve[ {eqn, bc} , theta, {t,0,tmax}]; (* We evolve from t=0 to tmax *)
(* At thus point soln$rules$list is {{theta -> InterpolatingFunction[{{0., }}, <>]}} *)
theta /. soln$rules$list[[1]] (* NDSolve always gives one solution, but you still have to ask for the first solution *)
];
phi = SHO$solution[3.14]; (* Try using the function we have just defined *)
(* phi is now an InterpolatingFunction, which can be evaluated, plotted, etc *)
phi[0]
0.5
phi[2.5]
-0.461702
Plot[ phi[tau], {tau,0,3.14}];
Like DSolve, NDSolve returns a list (of length 1)
containing a
list of substitution rules, one
for each unknown function in the differential equation.
In this case soln$rules$list[[1]] is a list containing one rule
that replaces instances of the unknown theta with the numerical
solution to the differential equation in the form of an InterpolatingFunction. To get that Interpolating Function we have to apply that rule to theta. Mathematica treats the Interpolating Function like a numerically defined function, so you can plot it, numerically integrate it, etc.
As we just saw, Mathematica expresses the solution of a differential equation as an InterpolatingFunction object. It is useful to be able to manipulate these, and to do so requires importing a special module called DifferentialEquations`InterpolatingFunctionAnatomy. With that in place, you can open up an InterpolatingFunction object and read off its properties.
ifn = Interpolation[ Table[ x=i/10.0; y=Sqrt[x]; {x,y}, {i,0,20}], InterpolationOrder->2]; (* Construct our own InterpolatingFunction *)
Plot[{ ifn[x],Sqrt[x]},{x,0,2}]; (* interpolation works well except near x=0 *)
(* Import the module that can look inside the InterpolatingFunction: *)
Needs["DifferentialEquations`InterpolatingFunctionAnatomy`"];
(* We can obtain the x limits over which the interpolating function is defined,
allowing us to plot it even if we didn't generate it ourselves *)
{x$min,x$max} = InterpolatingFunctionDomain[ifn][[1]]
{0., 2.}
Plot[ ifn[x], {x,x$min,x$max} ];
(* We can obtain the x-y points between which the function is interpolated *)
xvals = InterpolatingFunctionCoordinates[ifn][[1]]
{0., 0.1, 0.2, 0.3, 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1., 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2.}
yvals = InterpolatingFunctionValuesOnGrid[ifn]
{0., 0.316228, 0.447214, 0.547723, 0.632456, 0.707107, 0.774597, 0.83666, 0.894427, 0.948683, 1., 1.04881, 1.09545, 1.14018, 1.18322, 1.22474, 1.26491, 1.30384, 1.34164, 1.3784, 1.41421}
(* we can find out what order polynomial is used in the interpolation *)
order = InterpolatingFunctionInterpolationOrder[ifn][[1]]
2
(* we can switch the x and y data points to make a new InterpolatingFunction that is approximately the inverse of the original function *)
ifn$inverse = Interpolation[ Transpose[ {yvals,xvals} ], InterpolationOrder->2 ];
ifn$inverse[ifn[3.0]]
2.95755 (* The inversion is approximate *)
Unexpected errors can occur if we create functions that are numerically evaluated (using procedures like FindRoot or NIntegrate) and then try to use them like regular Mathematica functions. For example, consider a function that returns the root of a transcendental equation as a function of some parameter in the equation. First let's see that it cannot be evaluated symbolically:
trans$root[a_] = Module[{x},
x /. Solve[ x^3 - Tanh[x/a]==0, x]
];
Solve::nsmet: This system cannot be solved with the methods available to Solve.
OK, so we are forced to write it as a function that finds the answer numerically:
trans$root$numeric$naive[a_] := Module[{x},
x /. FindRoot[ x^3 - Tanh[x/a]==0, {x,1} ]
];
In this case we defined the function using delayed evaluation (:=) because it can only be evaluated once a number has been provided as the value of the argument a. The problem is, this function doesn't "know" that its argument must be a number. Errors will occur if we later use this function in a context where Mathematica tries to feed a symbolic value to the function. For example,
NIntegrate[ trans$root$numeric$naive[a], {a,1/2,1} ]
FindRoot::nlnum: The function value {1. - 1. Tanh[1./a]} is not a list of numbers with dimensions {1} ...
This surprising error arises because Mathematica, even though it
has been asked to
evaluate the integral numerically, attempts some symbolic manipulation
of the integrand, which is a purely numerical function.
To prevent this, we must define the function
so that it only accepts numbers as arguments.
To do this we add a _?NumericQ Pattern in the definition:
trans$root$numeric[a_?NumericQ] := Module[{x},
x /. FindRoot[ x^3 - Tanh[x/a]==0, {x,1} ]
];
NumericQ is a function that returns True if its argument is a number. a_?NumericQ is a pattern that says that
a can only be replaced with a number. The function will now only
accept numbers as arguments, and can be numerically integrated without error messages:
NIntegrate[ trans$root$numeric[a], {a,1/2,1} ]
0.472751
Mathematica has various fitting functions, such as Fit and FindFit, but the most powerful is NonlinearModelFit. Here is an example where we use it to fit a nonlinear function (a + b*Cos[omega*t]) to data. The three fit parameters are the vertical offset a, the amplitude b of the cosine, and the frequency omega of the cosine.
xydata = {{0., 0.951}, {0.1, 0.846}, {0.2, 0.309}, {0.3, -0.095}, {0.4, -0.694}, {0.5, -1.029}, {0.6, -0.706}, {0.7, -0.448}, {0.8, 0.768}, {0.9, 1.171}, {1., 0.963} };
nlmfit = NonlinearModelFit[ xydata, a + b*Cos[omega*t], {{a,0.2}, {b,1.0}, {omega,5}}, t]; (* we give an initial guess for each parameter *)
NonlinearModelFit can be rather sensitive to the initial guesses for the parameter values. If the fit is successful then
nlmfit is now a FittedModel object, which superficially behaves like the best-fit function to the data, but also contains a lot of information about the fit.
Normal[nlmfit] (* shows the best fit function *) 0.0707912 + 1.01908 Cos[6.44376 t] nlmfit[0.75] (* evaluate the best fit function at t=0.75 *) 0.193222 (* We can make a plot of the data and the fit: *) plot$data=ListPlot[xydata,DisplayFunction->Identity]; plot$fit=Plot[nlmfit[t],{t,0,1},DisplayFunction->Identity]; Show[{plot$fit,plot$data},PlotRange->{-2,2},DisplayFunction->$DisplayFunction];
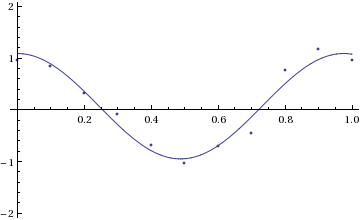
We can also extract information about the fit:
nlmfit["BestFitParameters"] {a -> 0.0707912, b -> 1.01908, omega -> 6.44376} nlmfit["ParameterErrors"] {0.0621924, 0.0790336, 0.162831} (* a is not significantly different from 0, but b and omega are *) nlmfit["ParameterTable"] Estimate Standard Error t-Statistic P-Value a 0.0707912 0.0621924 1.13826 0.287949 b 1.01908 0.0790336 12.8943 1.23746*^-6 omega 6.44376 0.162831 39.5732 1.82829*^-10 nlmfit["AdjustedRSquared"] 0.940382We can obtain many other diagnostics and properties of the fit, including an ANOVA table. See the Mathematica documentation for full details.
